The 8 Queens Problem : An Introduction¶

8 queens is a classic computer science problem. To find possible arrangements of 8 queens on a standard $8$ x $8$ chessboard such that no queens every end up in an attacking configuration. Now, if one knows the basics of chess, one can say that a queen can travel either horizontally, vertically, or diagonally. Hence, for 2 or more queens to be in an attacking state, they have to lie either horizontally or vertically or diagonally in-line with the other queen. The figure on the left illustrates that what all are the attacking positions with respect to a queen. As seen, the attacking positions are those where in the queen can move either horizontally, vertically, or diagonally along the chessboard.” $OK$ ” resembles the chessboard square which is considered a safe and non-attacking position. Whereas the one marked with an ” $X$ ” is an attacking placement. The figure on right, shows one of the possible arrangements that serve as a solution to the 8 queens problem.

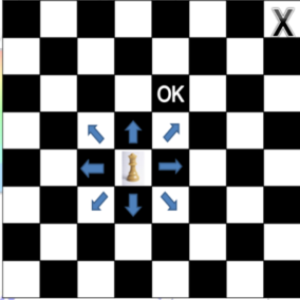
Images taken from chegg.com and indiamedic

There are various methods to solve the 8 queens problem. The most common being BackTracking. It can also be solved using a variety of approaches such as as Hill climbing, Genetic Algorithms - evolution, etc. In this post, I’ll explain how we approach 8 queens problem using Genetic Algorithms - Evolution.

First, a bit of Biology…¶

Yea.. I know,. Why Biology ? Well, get used to the hard truth. Most of our intelligence algorithms are made by ripping off nature. Be it neural networks or simple fibonacci sequence, our great mathematical models are merely a derivative of nature. But this does not make it any less valuable. Rather as my friend says, “Math is the universal language”. (I hope he reads this article) So yea, a bit of biology.

Let’s begin with basic cells and their multiplication and some genetics.

Consider 2 cells. Each cell has something called as pairs of chromosomes. A chromosome is what carries the genetic traits. The pairs and number of chromosomes isin’t much of relevance. What is important is how the process of cell production causes the genes to propagate into an offspring. This method is called as meiosis. Well, there’s another way called as mitosis, but in mitosis, there is no genetic diversity that is being propagated (Explained later in post). Till now we have established that the cells contain pairs of chromosomes. And that 2 cells are required for essential cell division.

Given below is an illustration as to how the division takes place. (Image taken from askabiologist.com)

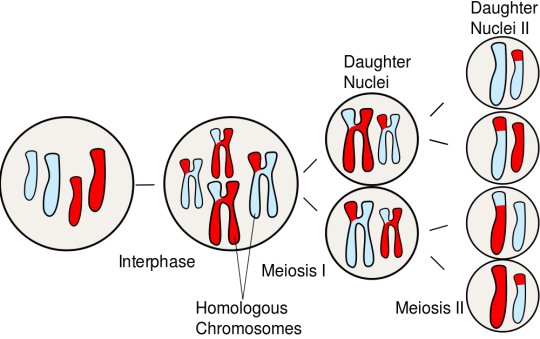
Process of meiosis. celldv1

Chromosme crossover

Crossover - In Detail: When 2 cells meet, the respective chromosome from cell1 and cell2 come together and mix. The mixing involves random parts of chromosome1 to get over-written by chromosome2. And the same in case of chromosome2. Hence, we are left with an inter mixed pair of chromosomes. Since chromosomes are carriers of genetic material, when there is mixing and intermingling of 2 chromosomes, there is also creation of new genetic sequences. Hence, this ensures genetic diversity. The formation of a more dominant / enhanced trait or a relatively sober trait can be attributed to such crossing over of chromosomes. Once crossover is through, the new offspring contains mixed characteristics for both the parents.

Then what is mutation ? : In rare cases, when the crossing over causes some unexpected trait to be formed. This is termed as mutation. Statistically, mutation is very rare. A common example for mutation is cancer. Mutation can be either good or bad. Even evolution is a result of mutation. Single celled organisms have mutated to form multi-celled organisms and so on ....

Once the simple process of cell reproduction is complete, we have a brand new offspring. The offspring contains traits of both the parents in random proportions. Similarly, many parents create multiple offspring, each offspring containing their traits. This set of offspring can be termed as a generation. We call it first generation. Again, when these offsprings (children) become parent , and produce their own offsprings, it gives rise to generation 2. Hence, when the process continues to go on, every generation can be said to have characteristics of the previous generation. Since the previous generation has characteristics of its’ previous generation, we can say that any randomly picked generation will have characteristics from all the previous generations.

The CS Stuff !!¶

Now where do we apply all this biology ? Just as we have an offspring which is equivalent to a weighted addition of the characteristics of the two parents, similarly, a chessboard with a certain arrangement of queens can be said to be an offspring of 2 parent chessboards that may have similar arrangements. For example, suppose we have 2 parent chessboards (C1 and C2). And on reproduction, C1 and C2 produce the offspring chessboard OC. Based on the aforemention biological evidence, I can say that

$$ OC = f(C1, C2) $$

where $ f( )$ is simply a function that combines random characteristics of C1 with the remaining characteristics of C2.

So any chessboard arrangement of 8 queens can be computed as selections of certain arrangements from C1 and C2. Thereby, asserting the fact that I am creating OC through random probabilistic selection and not any pre-processed criteria. This is strictly following the model prescribed by nature. By keeping everything random, we are essentially replicating the random “crossing over of genes” that occurs in cells.

**Core Working: **

Initialization : The initialization contains of the randomly distributed population that is generated. Lower population size will lead to lots of time in computation of approximate solution. And higher value will cause internal iterations to increase. Therefore choose population size carefully. In this example we have tried with population size of 100 , 500 and 1000
Selection of parents: Just as evolutionary biology requires two parents to undergo meiosis, so does GA. Therefore there is need to select two parents which determine a child. The calculation in determining the parents is elaborated later
CrossOver / Reproduction : Once parents having high fitness are selected, crossover essentially marks the recombining of genetic materials / chromosomes to produce a healthy offspring
Mutation : Mutation may or maynot occur. In case mutation occurs, it forces a random value of child to change , thereby shifting the algorithm in either a positive or negative route
Generation of new population : For all population, a child must be computed. Therefore, the new population can be said to be a list dynamically populated by the children computed.

The Algorithm:¶

function Genetic-Algorithm( population, Fitness-fn) returns an individual
    inputs: population -> set of individuals
            Fitness-fn -> a function that measures the fitness of an individual

    repeat
        parents <-- Select parents from Population
        population <-- Offsprings created by parents

    repeat until desired fit individual is obtained

return the best individual in the population

Above is a simulated evolution algorithm that mimics production of offspring generation from a given population. The population refers to the possible inputs.The population can be defined as simply a collection of many individuals. So it simply means, all possible arrangements of the queens on a chessboard. Consider this. Just as every human being can be defined by the presence of characteristics, any solution to the 8 queens problem can be defined by the placement of the queens in non attacking arrangements. Hence, each parent is a chessboard having some arbitary arrangement of the queens. Moving on, every individual can be regarded as a strong offspring or a weak one. We measure stregth of a human offspring through physical strength, immunity, etc. Whereas in the case of 8 queens, the fitness of a board arrangement can be considered as the number of clashes that take place between the queens. So the measure of fitness of any individual (chessboard arrangement) is attributed to number of clashes amongst attacking positions of queens.

**Fitness fn : ** I said that the fitness fn is proportional to the number of clashes amongst the queens. If seen, there are 28 clashes possible in an 8 x 8 chessboard. Therefore, if an individual has high fitness, I can say that it will have lower number of clashes.

$$ \text{Let clashes} = \text{number of clashing queens}$$

$$ \therefore fitness = 28 - clashes $$

Then, any individual with the maximum fitness will be having least number of clashes.

Implementation :¶

You can checkout my implementation here

** Setting up population ** : Your population is eventually going to determine the output. Each individual of the population is a board arrangement. So, firstly let’s describe the individual

BoardPosition :
    Attributes : 
        - Sequence
        - Fitness
        - Survival

def generateChromosome(): # randomly generates a sequence of board states. global nQueens init_distribution = np.arange(nQueens) np.random.shuffle(init_distribution) return init_distribution def generatePopulation(population_size = 100): global POPULATION POPULATION = population_size population = [BoardPosition() for i in range(population_size)] for i in range(population_size): population[i].setSequence(generateChromosome()) population[i].setFitness(fitness(population[i].sequence)) return population

As seen, each board position contains a sequence : the arrangement of queens on the board. A fitness value ( as discussed above) and a survival value. We need a survival value simply because evolutionary primitives say so. According to Darwin’s theory, ‘Survival of the fittest’, each parent (board position) has to be able to survive. This survival influences the ability of the parent to reproduce.

** Determining Fitness **

Secondly, we define a fitness function. As discussed above, we shall characterize fitness as a maximum value. Even though less number of clashes mean higher fitness , for implementation purposes, we consider maximum values of fitness. This can be done becuase we subtract number of clashes from 28.

To determine clashes, each queen has to be checked for

Row clashes
Column clashes
Diagonal clashes

The ideal case can yield upton 28 arrangements of non attacking pairs.

Therefore max fitness = $ 28.$

Hence fitness val returned will be $ 28 - \text{<number of clashes>}$

clashes = 0;
# calculate row and column clashes
# just subtract the unique length of array from total length of array
# [1,1,1,2,2,2] - [1,2] => 4 clashes
row_col_clashes = abs(len(chromosome) - len(np.unique(chromosome)))
clashes += row_col_clashes

# calculate diagonal clashes
for i in range(len(chromosome)):
    for j in range(len(chromosome)):
        if ( i != j):
            dx = abs(i-j)
            dy = abs(chromosome[i] - chromosome[j])
            if(dx == dy):
                clashes += 1


return 28 - clashes

** Determining Survival of individual **

Having demostrated how to calculate the fitness value, we can now move on to defining a survival function. A survival function will determine as to how able is a particular parent to survive and produce a healthy offspring. If out of 1000 people, the probability of any random person getting picked is $ \frac{1}{1000}$, similarly, the survival function can be written as a normalized probability of a individual getting selected based upon the fitness :

$$ \text{Survival for} i^{th} \text{individual} = \frac{f_i}{\sum_{j=1}^{j=populationSize} f_j } $$

** Selection of Parents & Crossover**

Parent selection is quite straightforward. Simply selecting 2 random - non equal parent will do the trick, but is very inaccurate and time costing. Hence, by using the survival function, elimination of weaker parent can be performed. Eventually, the parents left will be ones that are more likely to produce a fit offspring. Analogous to biology, two dominant traits will more likely produce a dominant trait cause it won’t matter which of the dominant trait is selected.

Once two parents are selected, the proceeding part is crossover. Crossover involves selecting a part of parent 1 and concatenating it with parent 2. Why … Because our chromosomes do so. This selective addition of chessboard board sequences will create an offspring that may have one of these three characteristics

It may either be a solution to the 8 queens problem. In that case, save the output and discard those parents –> child path.
It may have a higher fitness than either parent. This will also help in its survival
It may have a lower fitness value, thereby lowering its survival

Any of the three cases is still capable of producing a next generation. The only difference will be regarding the probability of that offspring to yield a substantially fit offspring.

**Mutation : ** Biologically and statistically, mutation is continously occuring at very low frequencies. In human genetic theory, mutation involves alteration within the structure of the chromosome, within the structure of the gene. To replicate this for 8 queens problem, one can simply alter a board arrangement.

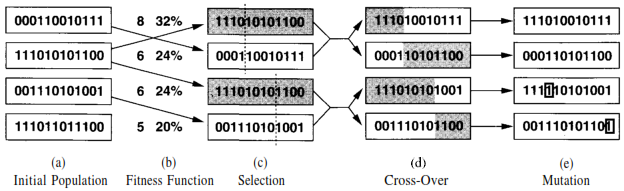
Source : Peter norvig genetic algorithm illustration

The above illustrates the entire flow from initial population to fitness function calculation, to selection to cross-over and finally mutation. Note : Mutation may or may not provide with the solution.

How to interpret input and output sequences:¶

Each row of the chess row is indexed from $0 \text{->} 7$ . The sequence $[\text{ a b c d .... }]$ means that in $0^{\text{th}}$ column, $a^{\text{th}}$ row, the queen is present and so on. The following are example sequences that are (not) a solution to the problem.

$[\text{1 1 1 1 1 1 1 1}]$ : This is certainly not a solution. All queens lie in the $1^{\text{st}}$ row of the board. Hence all are conflicting
$[\text{1 1 0 4 2 1 2 4}]$ : Similarly, thi aint a solution either.
$[\text{1 6 2 5 7 4 0 3}]$ : This satisfies 8 queen problem and hence a solution.

Output and termination criteria :¶

Well, it seems that such an algorithm will keep producing offsprings and again their offsprings. When to stop. In my implementation , I’ve kept a limit of iteration. This is just for purposes of conviniece. However, at anytime, the most optimal solution can be described as the most fit board position.

You can check out the code at Github.

Solving 8 Queens using Genetic Algorithms - Evolution